목차
Neural Network Basics
Binary Classification
-> 이진 분류
뭐가 맞다 아니다 => 1, 0으로 나타낼 수 있는것을 구별하는것
이런 이진분류를 한번 해보도록 하자.
일단 첫번째로 입력과 출력이 필요하다.
이런 하나의 입력과 출력을 training set이라 하고
$$ (x, y) \to x \in \mathbb{R}^{nx}, y \in {1, 0}$$
라고 말할 수 있다.
이진분류를 이미지로 나타내면 training set은 어떻게 구성될까?
먼저 이미지가 어떻게 표현되는지 알아야 한다.
이미지는
$$ n \times m$$행렬로 이루어져 있고
빨강, 초록, 파란색의 3원색이 각각 어떤 값을 갖고 있는지를 저장한다.
이를 훈련예제로 옮기면
각각의 행렬을 하나의 열벡터로 만들고
이 세개를 이어서 하나의 열벡터로 만든다
그러면
$$ x = \left[ \begin{array}{clr} \left[\text{red column vector} \right] \ \left[\text{green column vector} \right] \ \left[\text{blue column vector}\right] \end{array} \right] $$
이런 형태의 $$x$$가 만들어진다
이런 열벡터가 여러개 있을때
$$ m \text{ training example} = \left(x_1, y_1\right),\left(x_2, y_2\right), \cdots ,\left(x_m, y_m\right) $$ 이라고 한다.
이를 행렬로 나타내면
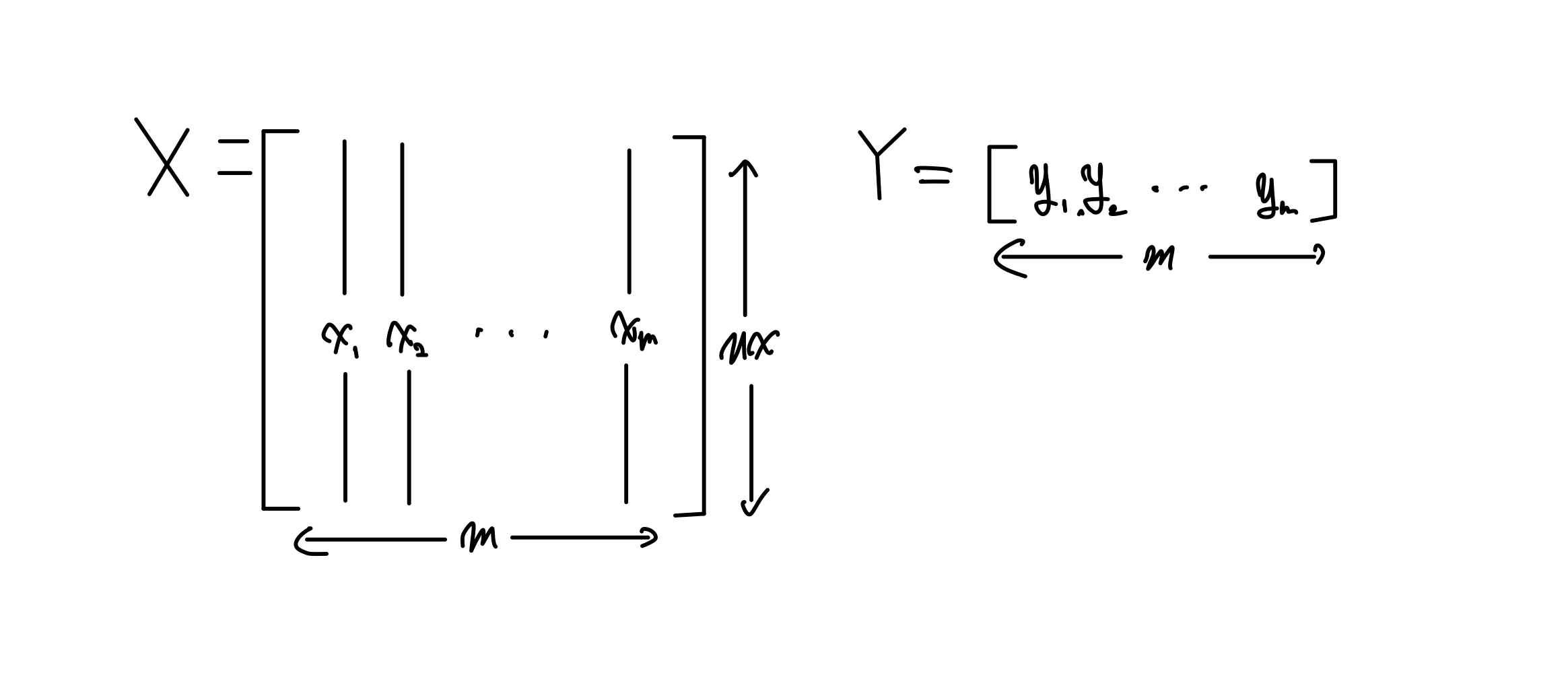
이렇게 나타낼 수 있다.
Logistic Regression
이진 분류를 구현하기 위해logistic regression(로지스틱 회귀)를 사용한다.
이 로지스틱 회귀는
$$x$$ 를 받아서 예측값 $$ \hat{y} = P\left(y = 1 \vert X\right) \[12pt] 0 \le \hat{y} \le 1 $$ 를 출력한다.
이때 이 함수의 파라미터는 $$ \text{parameter} = w \in \mathbb{R}^{nx}, b \in \mathbb{R} $$ 이다.
이 $$\hat{y}$$를 구하는 함수는 $$ \hat{y} = \sigma\left(w^TX+b\right) $$로 이 함수의 그래프는 아래와 같다.
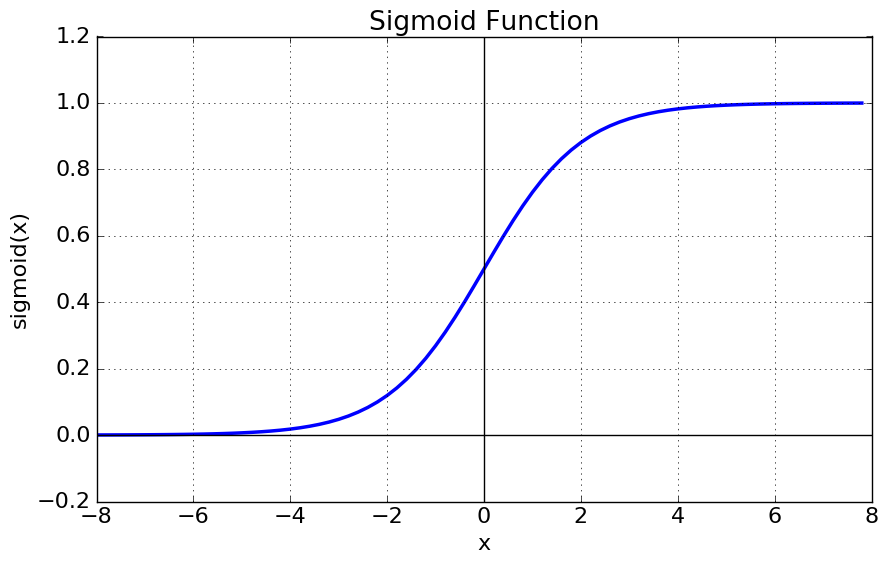
Logistic regression cost function
Loss function은 logistic regression으로 예측한 값과, 실제값의 차이의 지표를 나타내는 함수이다.
상황에 따라, 다양한 Loss function중 하나를 선택해서 사용하게 된다.
우리가 하는 이진분류에서는 cross entropy라는 loss function을 사용하게 된다.
그 함수는 다음과 같다.
$$ \mathcal{L}\left(y, \hat{y}\right): - \left(y\log{\hat{y}}+\left(1-y\right)\log{\left(1-\hat{y}\right)}\right) $$
하나의 training set에 대한것을 loss function이라고 하고, training example 전체에 대한것을 cost function이라고 한다.cost function은 loss function의 평균과 같다.
$$ \text{Cost function : } J\left(w, b\right) = \frac{1}{m}\sum_{i=1}^{m} L\left(y, \hat{y}\right) $$
Gradient Descent
Gradient Descent(경사하강법)은 cost function에 대한 그래프를 그렸을 때, $$w, b$$에 대한 cost function의 값이 가장 낮은 지점에 도달하게 parameter $$w$$와 $$b$$를 조정해 나가는 방법이다.
다음 그래프를 보자
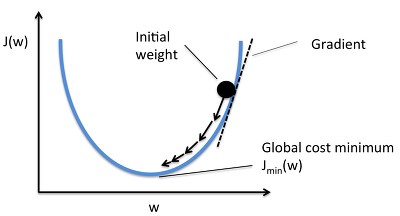
보기 편하게 하기 위해 일단 b를 생략하고 보자
cost function을 그려보면 이런 모양이 나온다.
여기서 $$w$$에 의한 한 지점에서의 기울기를 계산을 하면
가장 낮은지점보다 오른쪽에 있을때는 양수, 왼쪽에 있을때는 음수가 나온다.
이를 이용해서 기울기에 적당한 값을 곱해주고, 그 값을 $$w$$에 빼주는 형식으로 조정해 가면
가장 낮은 지점에 도달하게 된다.
계산 과정
$$ \frac{\partial\left(w, b\right)}{\partial w} = dw \frac{\partial\left(w, b\right)}{\partial b} = db $$
$$dw$$와 $$db$$는 표현을 저렇게 하는것이지 따로 수학적 의미가 있지 않습니다
$$w := w - \alpha \frac{\partial\left(w, b\right)}{\partial w}$$
$$b := b - \alpha \frac{\partial\left(w, b\right)}{\partial b}$$
두 식을 반복해주면서 점점 가장 낮은 값으로 이어간다
Computation Graph
하나의 예를 들어보자
$$ J\left(a, b, b\right) = 3\left(a+bc\right) $$가 있다
이때
$$ u = bc \ v = a + bc \ J = 3v $$
라고 하자
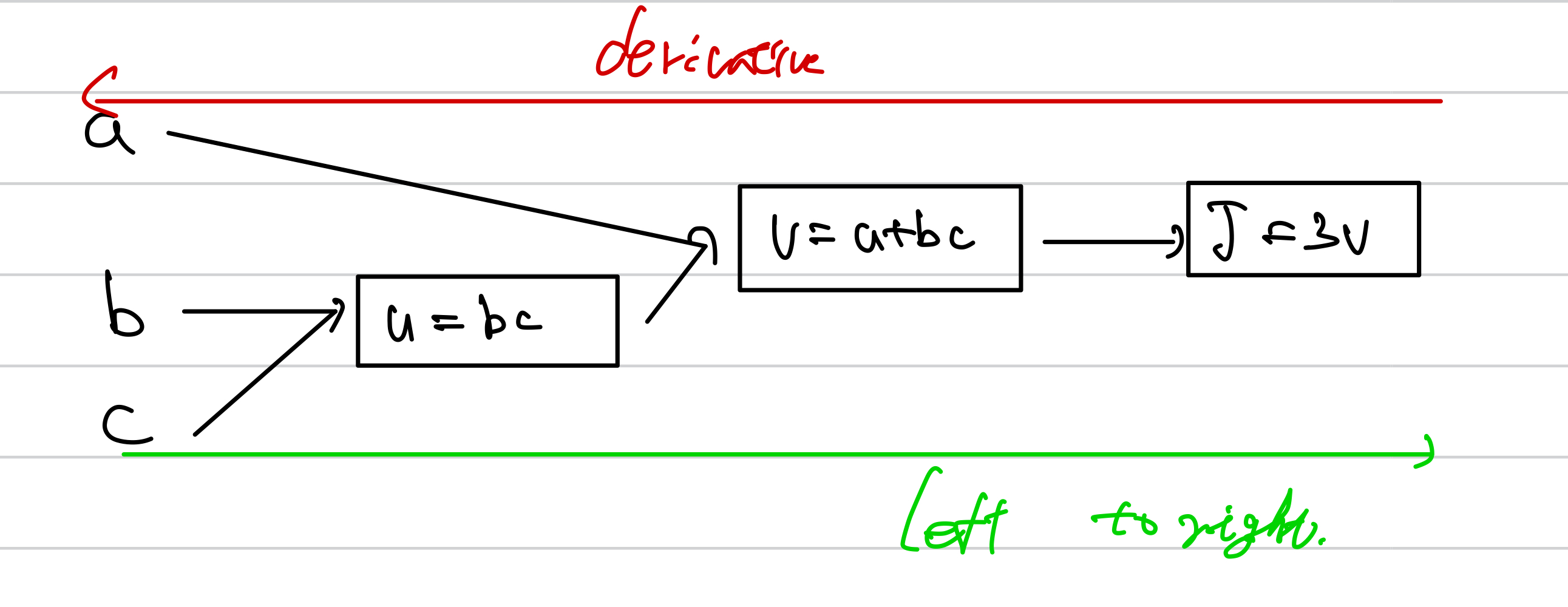
그럼 이렇게 나타낼 수 있는데
여기서 우린 $$ \frac{dJ}{da} $$를 순차적으로 구해나가볼 것이다.
먼저
$$ \frac{dJ}{dv} \frac{dv}{da} $$
를 순차적으로 구해나갈 것이다.
$$ \frac{dJ}{dv} = 3 $$ 이며, $$ \frac{dv}{da} = 1 $$이다
이를 연쇄법칙을 적용해보면 $$ \frac{dJ}{da} = \frac{dJ}{dv}\frac{dv}{da} = 3 $$ 으로 구할 수 있다.
그럼 이걸 적용시켜 보자
Gradient Descent with Logistic Regression
$$ z = W^TX + b $$
$$ \hat{y} = a = \sigma\left(z\right)$$
$$ L\left(a, y\right) = - \left(y\log{a} + \left(1-y\right)\log{\left(1-a\right)}\right) $$
를 구할 수 있다.
w, b 파라미터를 조정해줘야하므로dw, db를 구해서 w, b를 조정해 줄 수 있다.
아래는 $$ x_1, x_2 $$를 입력으로 하는 logistic regression의 전파과정이다.
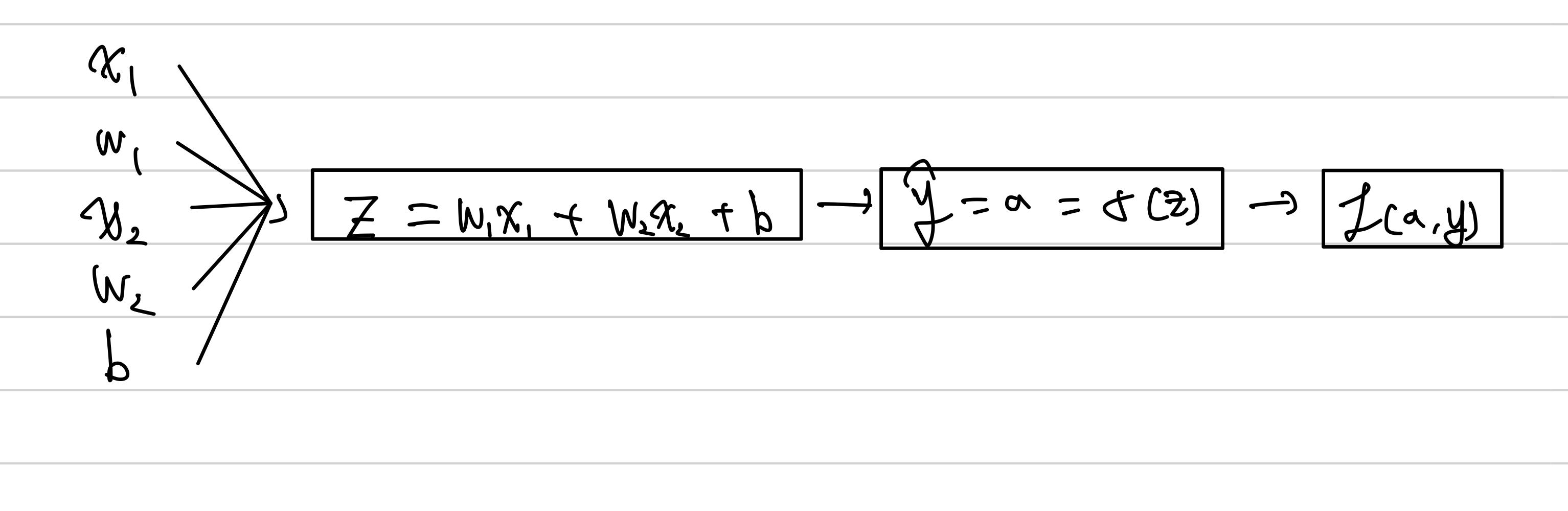
우리는
$$ w_1 := w_1 - \alpha dw_1 $$
$$ w_2 := w_2 - \alpha dw_2 $$
$$ b := b - \alpha db $$
이 과정을 진행해야하므로, 천천히 하나하나 구해주면 된다.
$$ "da" = \frac{dL}{da} $$
$$ \frac{dL}{dz} = \frac{dL\left(a, y\right)}{dz} \[8pt] = a - y \[8pt] = \frac{dL}{da}\frac{da}{dz} \[8pt] = "dz" $$
중간의 $$ = a - y $$는 $$ L\left(a, y\right) $$를 미분하면 나오는 공식이다
그 후
$$ "dw_1" = \frac{dL}{dw_1} = \frac{dL}{dz} \frac{dz}{dw_1} = "dz"X_1 $$
$$ "dw_2" = \frac{dL}{dw_2} = \frac{dL}{dz} \frac{dz}{dw_2} = "dz"X_2 $$
$$ "dw" = \frac{dL}{b} = \frac{dL}{dz} \frac{dz}{b} = "dz" $$
를 구해서 위의
$$ w_1 := w_1 - \alpha dw_1 $$
$$ w_2 := w_2 - \alpha dw_2 $$
$$ b := b - \alpha db $$
를 계산에 조정해나가주면 된다.
따로 부족한 부분이나 틀린점, 오타 지적은 댓글로 부탁드려요!
'부트캠프,프로그램 > Google ML Bootcamp' 카테고리의 다른 글
| 구글 머신러닝 부트캠프 2주차(1/3) (2) | 2022.09.02 |
|---|---|
| 구글 머신러닝 부트캠프 1주차(4/4) (4) | 2022.08.24 |
| 구글 머신러닝 부트캠프 1주차(3/4) (0) | 2022.08.22 |
| 구글 머신러닝 부트캠프 1주차(1/4) (0) | 2022.08.03 |
