세그먼트 트리(2021.03.27)

목차

세그먼트 트리

어떤 수들의 집합이 있다.
그 집합은 원소가 마구마구 변할 수 있다고 한다.

이 때, 그 집합의 부분합을 아주 빠르게 구하기 위해서 만들어진 구조이다.

예를 들어서..

1, 5, 6, 7, 4, 8, 2, 3

이렇게 수가 있다고 하자.

우리가 이 수들에서 특정 범위의 합을 구하려면 어떻게 해야할까?

역시 제일 간단한 방법은 다 더하는 것이다.

3~6번째 원소를 더하면.

6+7+4+8 = 25

이렇게 다 더하는 경우 시간복잡도는 O(N)으로 작은 범위 내에서 보면 나쁠 수 있다.

하지만, 이 합을 원하는 곳이 많아서 수천, 수만명이 요구를 한다면??
또, 이 데이터에 접근 가능한 사람이 많아서 계속해서 값이 바뀐다면??

참으로 난감할 것이다. 데이터는 바꿔줄 수 있지만.

합을 계속 해서 구하는것은 O(NM)의 시간복잡도로.. 상당히 힘들어 진다.

그래서 우리는 새로운 방식을 찾아야 한다.

어떻게 만들까??

이 문제를 세그먼트 트리를 이용해 해결할 수 있다.

세그먼트 트리를 이용하면,

합을 구하는데 시간복잡도가 O(logN)
값을 변경하는데 시간복잡도가 O(logN)으로,

많은 사람들이 요청해도 최악의 경우 O(MlogN)으로 상당히 빨라진다.

어떻게 만들까??

세그먼트 트리는 이진트리로,

세그먼트의 리프 노드에는 각 원소들이,
리프 노드가 아닌 내부 노드들에는 자식노드들의 합이 들어가게 된다.

예를 들면,

x~y 는 x부터 y까지의 합

이렇게 만들어주는 것이다.

그럼 만들어보자!!

만들기

만드는 방법도 알았으니 한번 만들어보자

언어는 c++로 택했다.
언어는 그렇게 중요하지 않다고 생각하니 한번 만들어보자.

먼저 세그먼트 트리를 만들어야한다. 데이터를 집어넣고, 트리를 만들어보자.

vector<int> tree;
vector<int> numbers;

/*
    start와 end는 지금 현재 노드의 범위를 뜻한다. 
    위의 예제로 보면, 루트노드의 start 는 0 end는 9이다.
*/
int init(int start, int end, int node){
    // start와 end가 같다면, 리프노드다. 리프노드에는 원소를 저장한다.
    if(start == end) return tree[node] = a[start];
    int center = (start+end)/2;

    // 나머지 노드에는 두개의 자식노드(tree[node*2], tree[node*2+1])의 합을 넣어준다.
    return tree[node] = init(start, center, node*2) + init(center+1, end, node*2+1);
}

짜란~ 트리를 만들었다.

구간합 구하기

그럼 이제 구간합을 한번 구해보자. 구간합의 시간복잡도는 O(logN)이라고 했다.

어떻게 그렇게 되는 걸까??

위의 예제에서 2~7까지의 합을 구해야한다 하자.

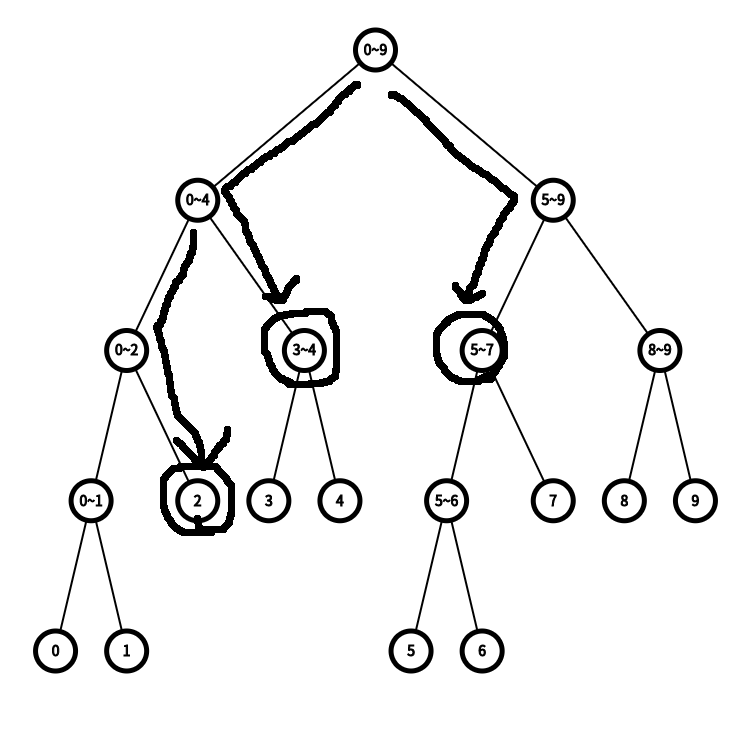
그럼 이렇게 3개의 합만 더해주면 되는 것!!!이다.

아주 간단하게, 단 몇번의 확인만으로 값을 구할 수 이따!!

//start, end, node는 만들때와 같고, left는 구간의 첫번째, right는 구간의 마지막이다.
init sum(int start, int end, int node, int left, int right){
    // 범위를 벗어나게 되면 으미가 업스므로 0을 반환..
    if(left > end || right < start) return 0;
    /*
        노드의 범위가 구하려는 범위 안쪽에 있다면 바로 반환해주면 되겠지??
        예제에서의 3~4노드, 5~7노드와 같다!!
    */
    if(left <= start && right >= end ) return tree[node];

    /* 
        만약 구하는 범위가 애매하게 걸칠때.. 
        위의 예제를 구하는데 0~4를 조사해버리면, 음. 0~1은 때버려야 구할 수 있다!!
        그러니까 한번 더 노드를 내려가서 검사하면 되겠다!!
    */
    int center = (start+end)/2;
    return sum(start, center, node*2, left, right) + sum(center+1, end, node*2+1, left, right);
}

좋아 그럼 합도 빠르게 구하는 법을 알아냈다!!

원소를 변경해보자!

그러나 이 원소가 막 바뀌면 어떡하지??
다시 처음부터 트리를 만들고, 합을 구하기에는 너무 시간이 많이 걸린다.

그래서 바뀌는 것도 빠르게 아주 빠르게 해야한다.

한번 예제에서 2를 바꿔보자.
2를 바꾸면 2를 포함하는 노드는 저어언부 바꿔줘야 한다.

처음부터 내려오면서, 2가 포함되어 있으면 2와 바꾸려는 수의 차이만큼 더해주고,

아니면 획 그냥 반환하는 식으로 2까지 바꿔주면 된다!!

void update(int start, int end, int node, int index, int diffrent){
    //범위 밖에있으면 버려주자!
    if(index < start || index > end) return;

    // 범위 안에있으면 차이만큼 더한다!!
    tree[node] += diffrent;
    // 마지막 리프노드까지 도달하면 끝!! 
    if(start == end) return;

    // 자식노드들도 다 바꿔줘야한다!!
    int center = (start+end)/2;
    update(start, center, node*2, index, diffrent);
    update(center+1, end, node*2+1, index, diffrent);
}

이렇게 바꿔주면, 역시나 한층 한층 내려가니까..

시간복잡도가 O(logN)!

계속 바뀌어도, 우리는 구간합을 아주 빠른 시간내에 구해 낼 수 있게되었다.

마무리

아직은 이걸 공부한지 얼마 되지 않았지만, 여러여러모로모로 쓸 수 있을거 같다.

그렇게 상상력이 좋지는 않아도 이렇게 생각이 드는거보면! 확실히 중요한 구조인거 같다...

열씨미 숙달할 수 있게 하자!

전체 코드

vector<int> tree;
vector<int> numbers;

/*
    start와 end는 지금 현재 노드의 범위를 뜻한다. 
    위의 예제로 보면, 루트노드의 start 는 0 end는 9이다.
*/
int init(int start, int end, int node){
    // start와 end가 같다면, 리프노드다. 리프노드에는 원소를 저장한다.
    if(start == end) return tree[node] = a[start];
    int center = (start+end)/2;

    // 나머지 노드에는 두개의 자식노드(tree[node*2], tree[node*2+1])의 합을 넣어준다.
}

//start, end, node는 만들때와 같고, left는 구간의 첫번째, right는 구간의 마지막이다.
init sum(int start, int end, int node, int left, int right){
    // 범위를 벗어나게 되면 으미가 업스므로 0을 반환..
    if(left > end || right < start) return 0;
    /*
        노드의 범위가 구하려는 범위 안쪽에 있다면 바로 반환해주면 되겠지??
        예제에서의 3~4노드, 5~7노드와 같다!!
    */
    if(left <= start && right >= end ) return tree[node];

    /* 
        만약 구하는 범위가 애매하게 걸칠때.. 
        위의 예제를 구하는데 0~4를 조사해버리면, 음. 0~1은 때버려야 구할 수 있다!!
        그러니까 한번 더 노드를 내려가서 검사하면 되겠다!!
    */
    int center = (start+end)/2;
    return sum(start, center, node*2, left, right) + sum(center+1, end, node*2+1, left, right);
}

void update(int start, int end, int node, int index, int diffrent){
    //범위 밖에있으면 버려주자!
    if(index < start || index > end) return;

    // 범위 안에있으면 차이만큼 더한다!!
    tree[node] += diffrent;
    // 마지막 리프노드까지 도달하면 끝!! 
    if(start == end) return;

    // 자식노드들도 다 바꿔줘야한다!!
    int center = (start+end)/2;
    update(start, center, node*2, index, diffrent);
    update(center+1, end, node*2+1, index, diffrent);
}